


进行建模时,总会涉及到与实际工程的对比,所建立的模型与实际情况越相近,那仿真出的结果越有工程意义。但是,有时为了某种目的,也需要人为的控制建模元素与实际情况的相似程度,甚至要切断所建立元素与模型的某些关联,达到某种理想状况,虽然与实际工程有一定差别,但是可以实现仿真目的。总之,一切建模的目的必须满足于本次仿真的需要,根据实际情况所需,确定选择什么样的手段。
Action only函数在约束方程中具备隔离标量表达式某些部分与约束反力的功能。通过对受约束系统的拉格朗日方程进行研究,可以很好地理解Action only函数的作用。
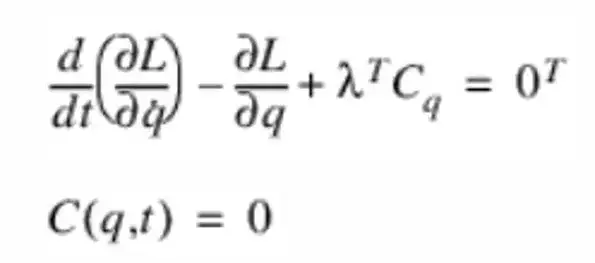
其中:
L为系统能量;
Q为广义坐标;
C为约束;
λ 为拉格朗日乘子;
通过拉格朗日方程可知,基于约束雅可比矩阵将约束反力投影到广义运动方程中,而基于Action only函数的机制,可以使某些选定的广义坐标免受约束反力的作用,从而实现数学上的隔离。
该函数只能用于约束方程表达式中,其形式很简单,AO(exp),表达式将标明哪些量同约束反力隔离。比如下面的示例:
描述Marker_1和Marker_2之间的约束方程如下所示:
GCON/1, FUN=DX(1) - AO(DX(2))
GCON/2, FUN=DY(1) - AO(DY(2))
GCON/3, FUN=DZ(1) - AO(DZ(2))
通过上述三条约束方程,实现两个点的平动位移绑定,如果不用AO函数,将实现同球铰一样的效果,但是这里使用了AO函数,表现出的效果为,约束反力仅会作用到Marker_1上,而不会作用到Marker_2上,从作用效果上看,就是实现了将Marker_1推向Marker_2,而不会有将Marker_2推向Marker_1的效果。相对比而言,不能使用下面的方式:
GCON/1, FUN=AO(DX(1,2))
GCON/2, FUN=AO(DY(1,2))
GCON/3, FUN=AO(DZ(1,2))
如果这样设置,在没有AO函数的情况下是可以的,但是使用AO函数的本质在于原本一个相互的效果要被隔离成单向的效果,所以会造成不能计算的现象。因为从DX(1,2)的角度要保持两个点的位移绑定,但是使用了AO函数,造成不能达到这个目的,因为约束反力不能施加于任何一个Marker点上,约束方程不能被严格满足,因此出现计算发散的问题。
比如飞行器飞行过程中,其姿态角度的获取,虽然有很多方法,这里3499拉斯维加斯官网采用AO函数的隔离效果进行检测。
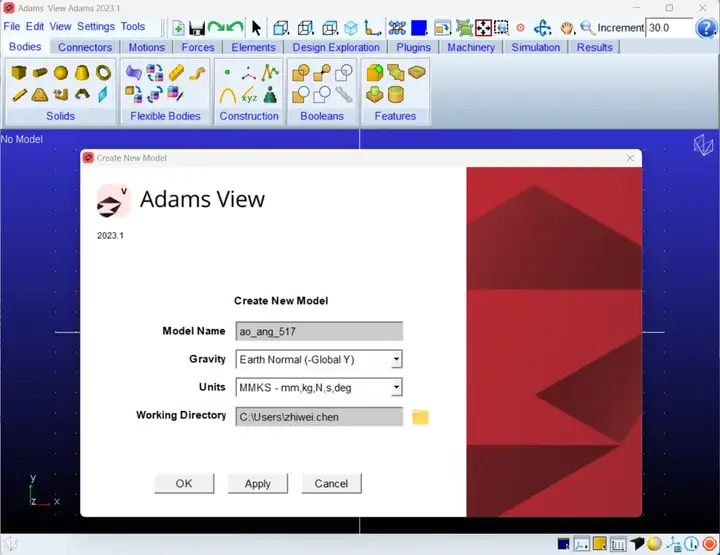
这里采用Adams最新版本2023.1完成实例说明,但是AO函数已经存在较长时间,前面的版本也适用。建模内容包括:
圆柱体和圆锥体两个部件,之间使用固定副约束;
在圆锥体质心上施加了侧向干扰脉冲信号,在给定时间完成作用;
在圆柱体的底端圆心施加推力,方向沿圆柱轴线;
在圆柱上再施加一个绕圆柱轴线的点驱动,转速30度每秒;
创建一个点质量,位于圆柱质心处,同时,施加自定义约束保证点质量与圆柱质心重合。
自定义约束如下:
dX(POINT_MASS_1.cm)-ao(dX(PART_2.cm))
dY(POINT_MASS_1.cm)-ao(dY(PART_2.cm))
dZ(POINT_MASS_1.cm)-ao(dZ(PART_2.cm))
之所以定义为上述形式,目的在于将点质量始终与圆柱体也就是part_2的质心重合。这样就可以使用点质量位置与圆柱体上的局部坐标系进行测量,方便测绘出其飞行过程中的所需角度值。
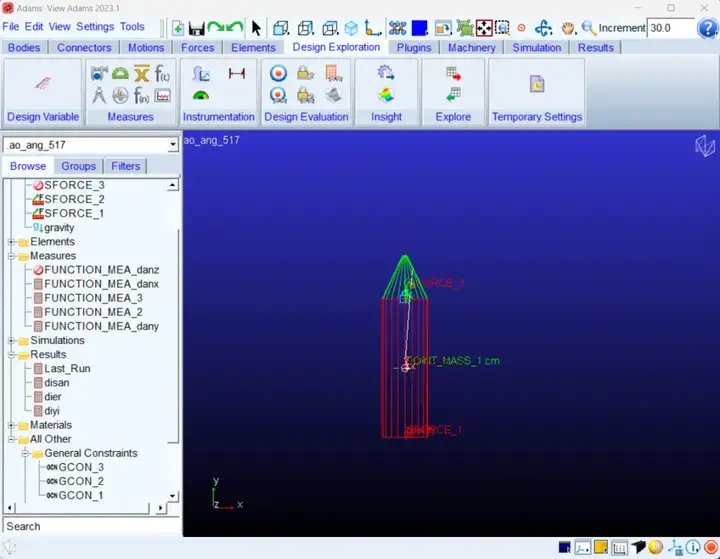
这里为了说明问题,仿真时将重力先关闭。对其进行了如下的测量:
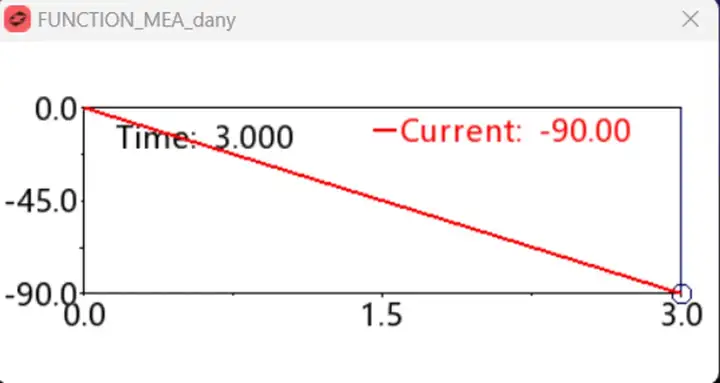
上图为基于AO函数实现的测量,测出的结果与实际施加的相同,30度每秒*3秒=90度。说明了该种方法的正确性。
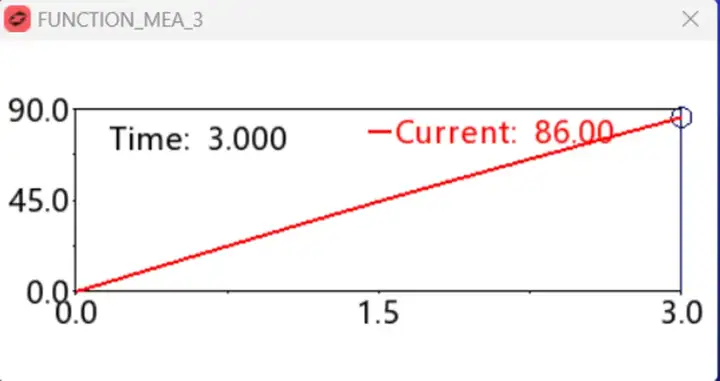
上图为直接通过AY函数对质心的简单测量,最终值为86度,明显与实际有差别。当然,该种简单方式,可应对单自由度作动状况下的角度测量,因为其基于全局坐标系完成。而本模型设定的为多自由度驱动,该方法不适用。如果约束方程不用AO函数,而是直接改写为如下状态:
dX(POINT_MASS_1.cm)-dX(PART_2.cm)
dY(POINT_MASS_1.cm)-dY(PART_2.cm)
dZ(POINT_MASS_1.cm)-dZ(PART_2.cm)
如前所述,这样类似于球铰,两个物体之间的相互作用力是完备的,从拉格朗日方程角度看,点质量对圆柱体的约束反力和圆柱体对点质量的约束反力都同时存在,两者之间有正常的力学作用效果,要实现两者广义坐标的同步运行,需要耗费更多的能量。如果是AO模式,则仅需要对圆柱体的广义坐标进行做功,虽然从动画上看,圆柱带动点质量一并运动,但是,由于AO函数的特殊机制,截断了圆柱体对点质量的力学影响,这一过程并不需要能量,完全是数学的机制而非力学机制。两种工况仿真结果的差别也可以在模型中表现出来,如下图所示:
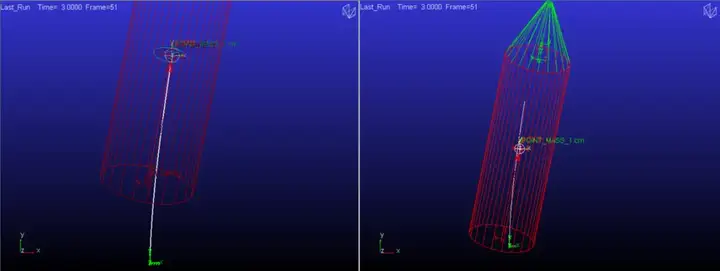
上图左侧为有AO的状态,右侧为没有AO的状态,仅仅这一个差别,造成模型最终的仿真状态有明显的差异,主要体现在圆柱体质心点的竖直位移上,这两幅图的白色轨迹线是完全相同的,即圆柱质心点的轨迹。问题的根源还在于AO函数的作用机制:没有AO的模型,由于点质量前面设置为10Kg(故意设置较重,效果更明显),此时约束反力相互作用下,推力相同,在3秒内完成相同的做功,其竖直方向的位移势必要小于有AO的模型。相当于,有AO的模式推动的质量为圆柱18Kg,圆锥2Kg,共计20Kg,而没有AO的模式还要再加上点质量的10Kg,共计30Kg。从图上也可看出,没有AO的模式圆柱质心点大约在轨迹线竖直方向的2/3处。
基于AO函数的特殊机制,结合自定义约束可以实现非常灵活的应用,当然,其应用更多不是为了模拟模型,而是为了其他目的,比如这里描述的测量或者其他,但其本质相同,就是要截断为了完成特殊目的而建立的元素对模型的影响,但是又能直接获取模型中的有用信息。Adams中还有许多类似的功能函数,仅仅通过一些简单的设置即可完成工程中非常实用的功能。因此,在Adams的使用过程中,对各种函数的掌握以及灵活使用,是一个不断积累的过程,可能一个很小的软件功能点,却可以解决实际工程中的一个关键问题。